caddywhe.blogg.se

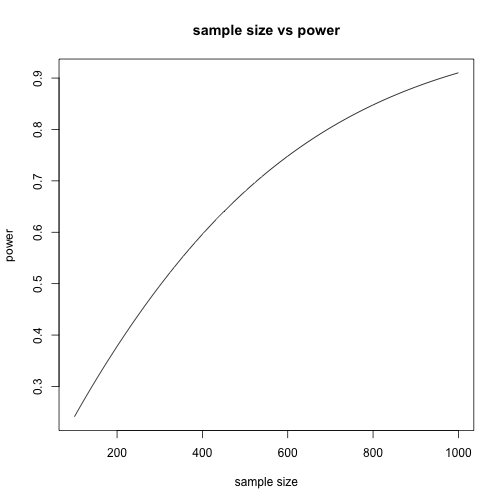
We can chart the power of the test for various values of p obs as shown in Figure 2.

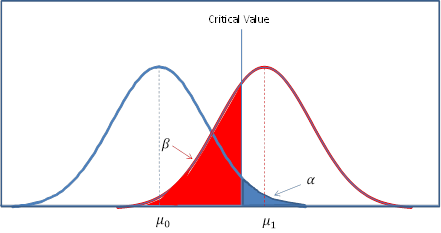
The power of the test is calculated using the following formula where p obs = 13/24 =. In fact, 95.8% of the distribution is found to the left of the critical value (inclusive) sinceīINOM.DIST( x crit, n, p, TRUE) = BINOM.DIST(12, 24. This means that at least 95% of the distribution occurs for values x ≤ 12. 05 based on the binomial distribution with null and alternative hypotheses:Īs in Statistical Power of a Sample, to find the power of this test we must first calculate the critical value. Power of a one-tailed testĮxample 1: What is the power of the test in Example 3 of Hypothesis Testing for the Binomial Distribution?įor this example we found 13 successes in a sample of size 24 and used a one-tailed test with α =. In addition to the approaches described on this webpage, for large samples, by Corollary 1 of Relationship between Binomial and Normal Distributions, a random variable which has a binomial distribution can be approximated by a normal distribution, and so the techniques described in Statistical Power and Sample Size can also be used directly. The process is similar, except that we need to take into account that the binomial distribution is a discrete distribution, unlike the normal distribution which is a continuous distribution. On this webpage, we show how to do the same for a one-sample test using the binomial distribution. In Statistical Power and Sample Size we show how to calculate the power and required sample size for a one-sample test using the normal distribution.